Data Structures and Algorithms: Graph Algorithms

Search Graph Algorithm
The Search Graph Algorithm are the algorithms to traverse through a Graph.These Algorithms systematically explores each vertex that is reachable from sourse. There are fundamentally two Search Graph Algorithm,Breadth First Search and Depth First Search,which traverse as the name apply.

Breadth First Search

The algorithm is named so as traverse through the graph breadth wise i.e. The algorithm discovers all vertices at distance K from sourse S before discovering any vertices at distance K+1. It computes the distance from source to all reachable vertices.

To keep track of progress ,it starts with all white vertices ,whenever it encounters a vertex it colors it red and later voilet. Breadth search search constructs a breadth first tree ,initially containing only its root ,which is the sourse vertex S.whenever a white vertex V is discovered in the course of scanning the adjacency list of an already discovered vertex U ,the vertex V and the edge(u,v) to the tree including the vertex U as parent of V.

The BREADTH FIRST SEARCH assumes that input graph G = (V,E) is represented as adjacency-list. The Algorithm is as follows.

Algorithm

1. for each vertex u belonging to V[G]-{S}

2. do color[u] <-- white

3. d[u] <-- infinity

4. #[u] <--NIL

5. color[S] <-- red

6. d[S] <-- 0

7. #[S] <--NIL

8. Q <--S

9. while Q != NULL

10. do u <-- head[Q]

11. for each V belonging to Adj[u]

12. do if color[V] = white

13. then color[v] <--red

14. d[v] <--d[v] +1

15. #[v] <-- u

16. ENQUEUE(Q,v)

17. DEQUEUE(Q)

18. color[u] <-- voilet

                                 The procedure of BFS is as follows . Line 1-4 paint every vertex white,set d[u] to infinity and parent of each vertex to NULL. Line 5-8 paints the sourse S gray ,initialies d[S] to 0,and its parent to NULL and add it to Q which contains set of gray vertices. The for loop of program is contained in Line 9-18. The loop iterates as long as gray nodes are present ,which are discovered during search of adjacency lists of vertices,Line 10 determine the gray vertex u at the head of Q.the for loop of lines 11-16 considers each vertex V in the adjacency list of u .If V is white ,then it has not been discovered and the algorithm discoveres it by executing lines 13-16. It is first grayed and its distance d[V] is set to d[u]+1.Then ,u is recorded as its parent .Finally it is placed at the tail of Q.when all the vertices of adjacency list of u are examined ,u is removed from Q and blackened in lines 17-18.
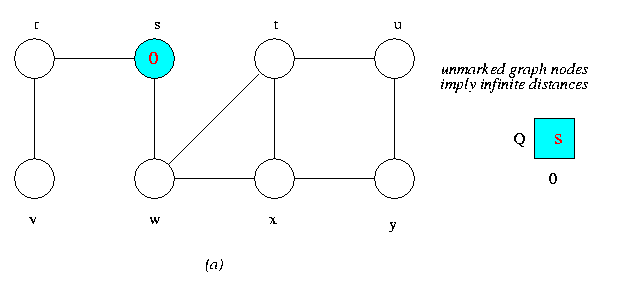
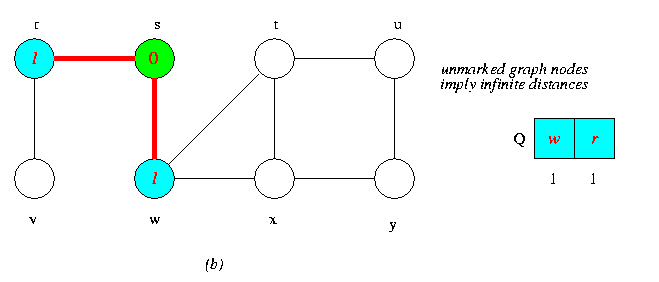
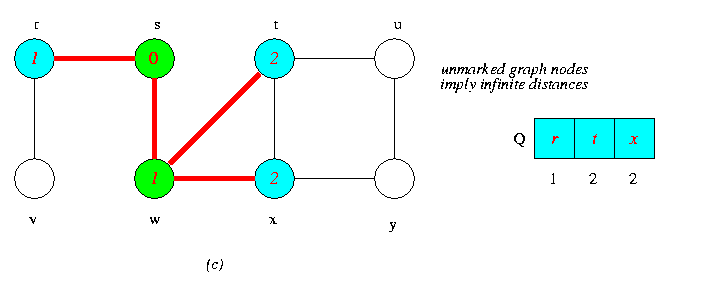
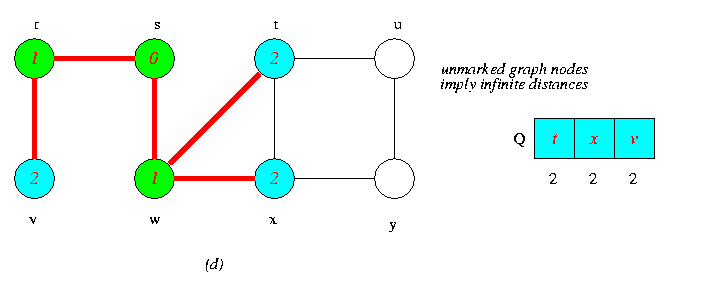
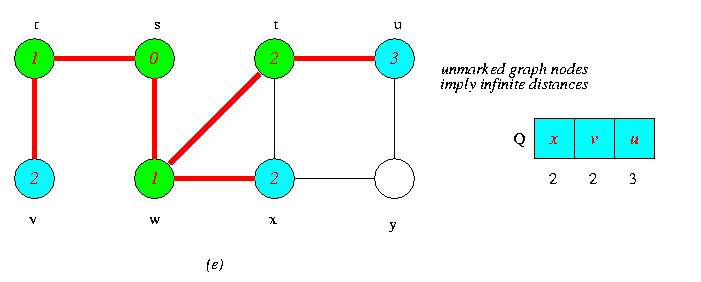
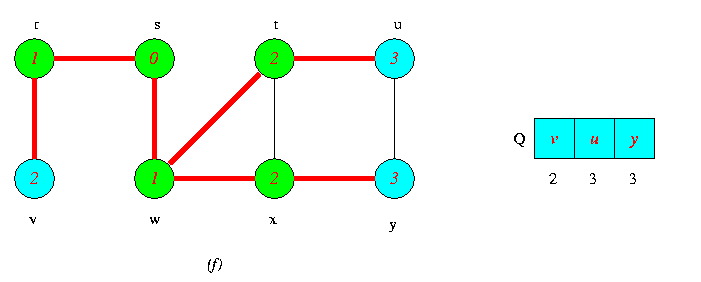
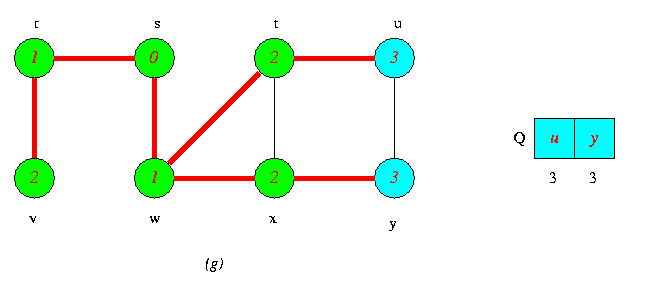
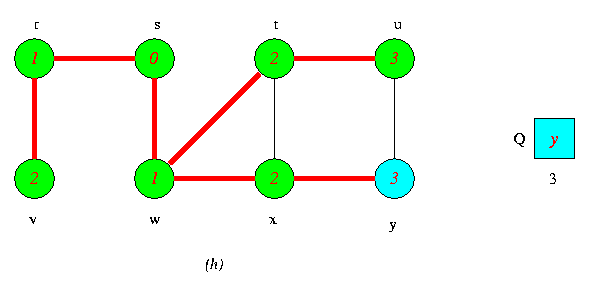
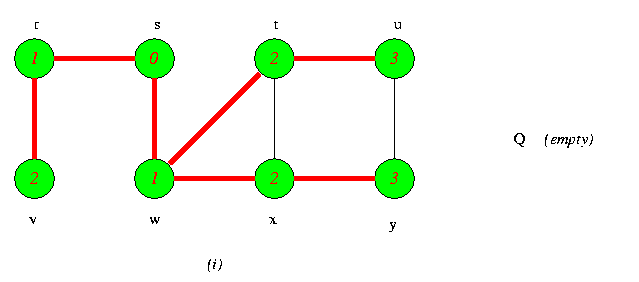
      Operations of BFS on an Undirected Graph
   Tree edges are shown red as they are produced by BFS. Within each vertex u is shown d[u].The queue Q is shown at the begining of each iteration of the while loop of lines 9-18.Vertex distances are shown next to vertices in the queue.

                                           Run Animation

Depth first search
The startegy followed by DEPTH FIRST SEARCH is, as the name imply ,to search deeper in the graph whenever possible. In depth first search ,edges are explored out of the most recently discovered vertex V that still has unexplored edges leaving it .When all of V's edges has been explored ,the search "back Tracks" to explores edges leaving the vertex from which V has been discovered .The process continues until we have discovered all the vertices reachable from the original source.The entire process is repeated until all the vertices are discovered.

Algorithm

                DFS(G)
                        1.    for each vertex u belonging to V[G]
                        2.             do   color[u]<--white
                        3.             parent[u]<--nil
                        4.    time <--0
                        5.   for   each vertex u belonging to V[G]
                       6.             do if   color[u] = white
                       7.                        then    DFS-Visit(u)

            DFS-visit(u)
                      1.    color[u]<--gray      |> white vertex has just been discovered
                      2.   d[u]<--time<--time+1
                      3.   for each V belonging to Adj[u]     |>    Explore edge(u,v)
                      4.              do if     color[V] = white
                     5.                            then   parent[V]<--u
                     6.                                            DFS-visit(V)
                     7.    color[u]<--black
                     8.    f[u]<--time<--time+1

        The procedur DFS works as follows .the Line 1-3 paint all vertices white and initialize their parent as NIL .Line 4 resets the global time counter .Lines 5-7 check each vertex in V in turn and when a white vertex is found,visit it using DFS-visit.Every time DFS-visit(u) is called in Line 7,vertex u becomes the root of a new tree in Depth First Forest.
        in each call DFS-visit(u) vertex u is initially white .Line 1 paints u gray ,and line 2 records the discovery time d[u] by incrementing and saving the global variable time.Line 3-6 examines each veretx V adjacent to U and recursively visit V if it is white . As each vertex V belonging to Adj[u] is considered in Line 3 ,Finally after every edge leaving the u has been explored ,Lines 7-8 paints u black and record the finshing time in f[u].
    The total cost of execution is of order of (V+E).

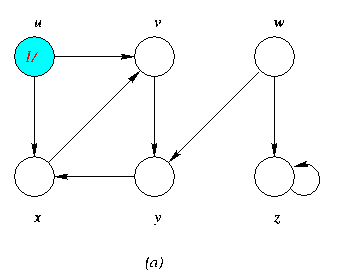
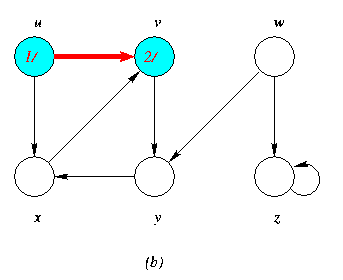
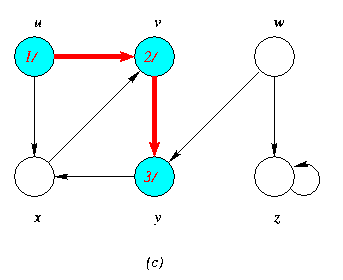
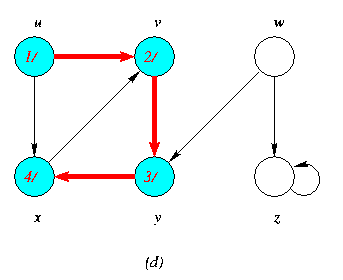
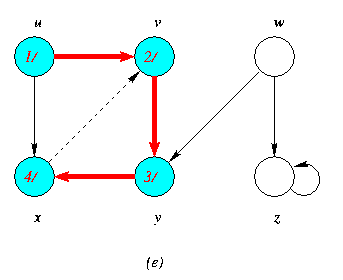
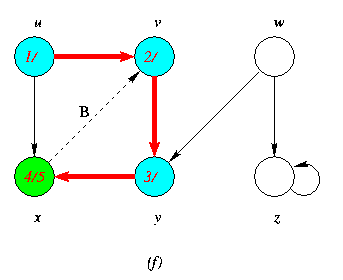
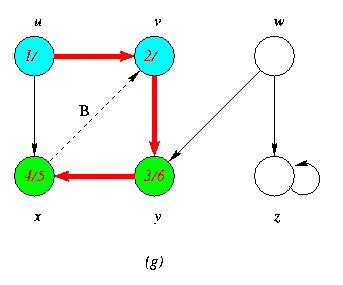
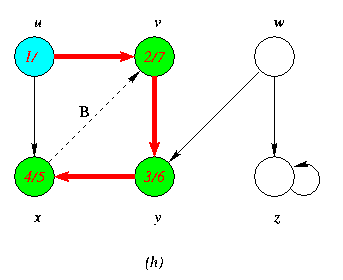
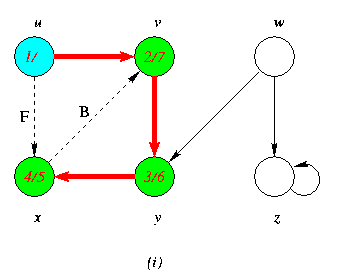
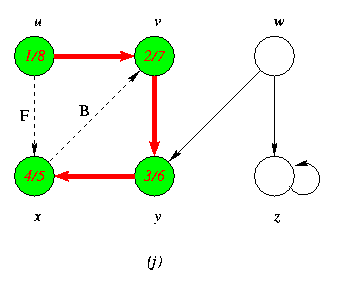
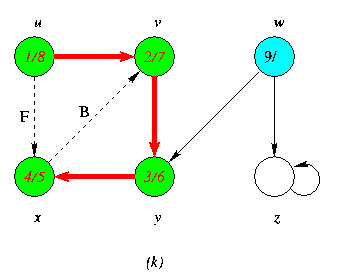
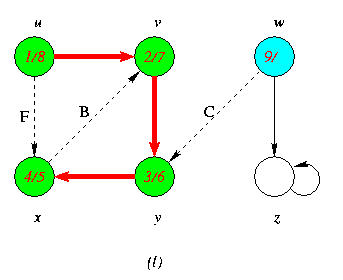
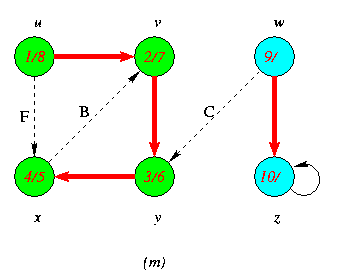
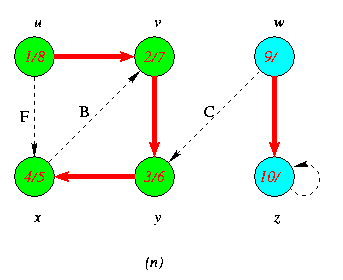
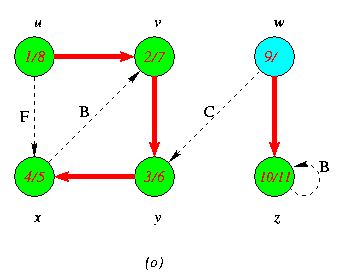
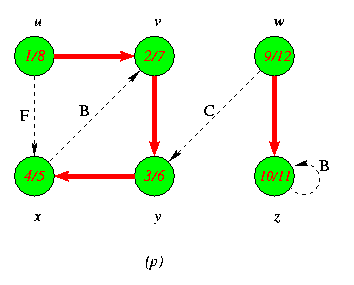
            Progress of Depth First Search DFS Algortithm on a directed Graph
      As the edges are explored by the algorithm,they are shown as either red (if they are tree edges ) or dashed (otherwise).Nontree edges are lebeled B,C or Fto wether they are back,cross or forward edges.Vertices are timestamped by discovery time/finishing time.

                        Run Animation


Key to Home

      Search Graph Algorithms
This Tutorial was written by Abhishek Goyal,Marghoob Mohiyuddin,Pooja Nath and Ruchi Saran Please email comments to:
[email protected] [email protected]